Rechercher
Accueil > La Recherche > Axes & Equipes > Physique Théorique > Equipe : Systèmes Complexes et Phénomènes Non Linéaires > Thème : Physique Théorique des Systèmes Biologiques
Density waves approach to the procapsid structure of small icosahedral viruses : Irreducible structures with icosahedral symmetry
publié le , mis à jour le

V.L Lorman [1] and S.B. Rochal [2]
Before starting the program, please, read attentively the user’s
note.
– The program generates the irreducible structures with icosahedral
symmetry on the spherical surface. For that purpose it restricts
the irreducible representations of the spherical rotational group
SO(3) to the icosahedral rotational group I (discrete group - composed of 60 rotations of an ideal icosahedron). Then it
constructs a continuous scalar density distribution on a sphere
invariant with respect to the group I.
– The irreducible representations of the SO(3) symmetry group are
labeled by an integer positive number l. Before starting the program you have to precise its integer value in the window Ir.Repr.Number. Its default value is chosen to be 6. The calculation runs when the key GO_1 (or the key GO_2) is pressed. On the first step the program calculates the number ![]() of totally-symmetric irreducible representations in the restriction
of totally-symmetric irreducible representations in the restriction
of the chosen irreducible representation upon the I symmetry group. This value is shown in the bottom of the screen frame. If it
is equal to zero then the representation with the integer number
you have chosen cannot generate any function invariant with respect
to the I group and the corresponding irreducible icosahedral structure does not exist. On the second step the program constructs the graphic image of the density distribution function presented in the form :
![]()
where
θ and Φ are conventional angular variables of the spherical coordinate system![]() are elements of the I
are elements of the I
symmetry group
and ![]() are the spherical harmonics.
are the spherical harmonics.
The integer positive variable ![]() is optimized by the program automatically.
is optimized by the program automatically.
– The buttons MAX and MIN permit to choose the type of the graphic presentation of the ![]() function before starting the calculation. For the sake of clarity the function
function before starting the calculation. For the sake of clarity the function ![]() is shown in the region where it is positive (button MAX was chosen) or where it is negative (button MIN was chosen). In the former case the program calculates the globally maximal value of the function
is shown in the region where it is positive (button MAX was chosen) or where it is negative (button MIN was chosen). In the former case the program calculates the globally maximal value of the function ![]() and assigns this (always positive) value to the variable A. In the latter case the
and assigns this (always positive) value to the variable A. In the latter case the
program calculates the globally minimal value of the function ![]() and assigns this (always negative) value to the same variable A.
and assigns this (always negative) value to the same variable A.
– The image can be cut off by two limit values CUT_min and CUT_max. The function ![]() is shown only in the region where CUT_min ≤
is shown only in the region where CUT_min ≤![]() ≤ CUT_max.
≤ CUT_max.
You have to chose the values of CUT_min and CUT_max (0 ≤ CUT_min ≤ 1 and CUT_min ≤ CUT_max ≤ 1 ) in the corresponding windows before starting the calculation. The default values of the variables CUT_min and CUT_max are 0 and 1, respectively. Finally,
the image of the normalized density function (![]() value) is shown using conventional color presentation : the growth of
value) is shown using conventional color presentation : the growth of ![]() value corresponds to the change of colors from red to violet. The constructed images are automatically saved in the current folder when the checked box ’To save the figures’ is switched on.
value corresponds to the change of colors from red to violet. The constructed images are automatically saved in the current folder when the checked box ’To save the figures’ is switched on.
– The checked box ’cubic set’ permits you to visualize the same image
along two different crystallographic directions. If the checked
box ’cubic set’ is switched on then the icosahedron 2-fold
direction is perpendicular to the image plane otherwise the image plane is perpendicular to the icosahedron 3-fold direction.
– To download this program, please see below. For the moment we can propose only the version for Windows (sorry for the LinuX user, they have to wait) .
– Remark : GO_1 and GO_2 buttons use ![]() functions with different m values in the group averaging procedure to obtain the function invariant with respect to the I group. If
functions with different m values in the group averaging procedure to obtain the function invariant with respect to the I group. If ![]() then the functions constructed by averaging GO_1 and by averaging GO_2 are linearly dependent. It is ensured by the group theory. From the practical point of view the functions coincide up to eventual multiplier equal to -1. If
then the functions constructed by averaging GO_1 and by averaging GO_2 are linearly dependent. It is ensured by the group theory. From the practical point of view the functions coincide up to eventual multiplier equal to -1. If ![]() then the functions
then the functions
constructed in two above-mentioned different ways are linearly
independent. The program can not construct all ![]() linearly independent functions in a case
linearly independent functions in a case ![]() .
.
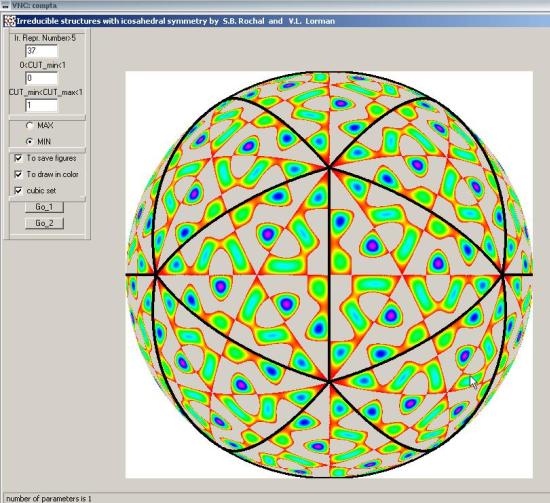
location of proteins in Murine Polyoma virus.
To construct this picture, please, introduce Ir.Repr.Number=37,
chose button MIN, and press G0_1.
Please, cite this site and our article ’[Lorman
V.L. and Rochal S.B., Density-Wave Theory of the Capsid Structure of Small Icosahedral Viruses]’ in your works.








